SMA Home
News
Phenomena
Model
Crystallography
Simulation
Applications
Research
Services
Publications
Contact
Links
On this site, we shall give a short review of a shape memory model which is well suited for control applications. It has been originally developed by Müller and Achenbach and describes the time-dependent thermomechanical behavior of an SMA wire. It is motivated by experimental evidence of the underlying micromechanics, and the resulting mathematical structure is given by a set of differential-algebraic equations, making it fit nicely into modern mathematical theories of optimal control problems.
The main feature of shape memory alloys used for actoric applications is the capability of strong contraction upon heating. This on first glance surprising behavior is explained by inspection of the micromechanics during such a process.
The basic mechanism is a phase transition in the crystal lattice structure. In the one dimensional case, a lattice particle does either exist as the highly symmetric austenite phase A, or as a sheared version hereof. This, we call a martensitic twin phase and denote it by M(+) or M(-), depending on the direction of shear. In the absence of external loads, martensite is stable at low temperature and austenite at a higher one. Observation of a specimen during the phase transition reveals a structure of alternating layers of austenite and martensite.
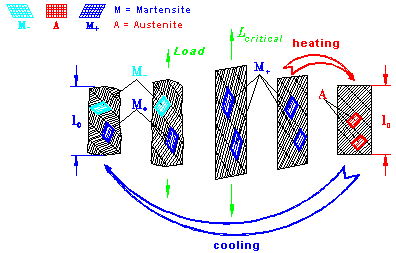
Figure 1 Layer structure of an SMA specimen and shape memory effect
The sequence of pictures in Figure 1 illustrates the behavior of these layers in a tensile experiment. Initially, at low temperature, the body is in a martensitic state, half of the layers M(+), the other half M(-). Application of a tensile external load first causes the layers to straighten, and, at a critical load level, the M(-)-layers flip into the M(+)-phase, thus contributing to a considerable length change. Upon removal of the load, the M(-)-layers do not flip back into their original phase, but when the specimen is heated, all the layers transform into the unsheared austenitic phase. This causes the body to shorten again and thus gives rise to the well-known shape memory effect. Subsequent cooling finally completes the cycle by having the martensitic twins occur again.
In order to describe the above behavior, the model takes the metallic layers as basic elements. The total length change of the wire is calculated as the sum of the length changes of the individual layers
D=N{xA(D A)+x+(D +)+x-(D -)}. (1)
N is the total number of lattice layers, xA, x+ and x- denote the volume fractions of the corresponding phases, and the bracketed quantities are the expectation values of the length changes in the phases. They are calculated from statistical thermodynamics, e.g.
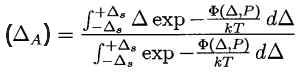 (2)
(2)
In equation (2), T is the wire temperature, k is Boltzmann’s constant and F(D ,P) is the potential energy seen by a layer. It depends on the layer shear length D and is given by a triple-well function with each well corresponding to one of the three phases, see Figure 2. In the presence of an external load, this function has to be superposed by the work done by the load, which in the one dimensional case simply is – PD .
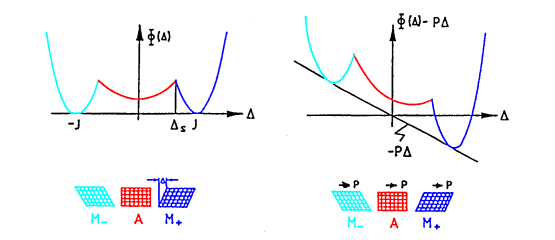
Figure 2 Three phases of a lattice particle and corresponding potential energy.
For the determination of the phase fractions the model assumes the shear lengths of the layers to fluctuate about their equilibrium values in the potential wells. Occasionally, the layers are able to overcome the barriers between the wells, and this gives rise to time rates of change for the phase fractions x+ and x- according to
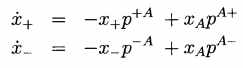 . (3)
. (3)
The quantities pab are the transition probabilities from phase a to phase b , which also can be calculated from statistical thermodynarnics, e.g.
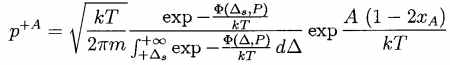 . (4)
. (4)
In equation (4), A is an interfacial energy coefficient responsible for the alloy’s hysteretic behavior and m is the mass of a layer.
A variant of this model is introduced, which is based on an approximate evaluation of the integrals giving the possibility of high speed computations. Such calculations provide a good overview of the features of the model like the strong temperature dependence of its load-deformation behavior. Furthermore an extension of the model has been given incorporating the possibility of electric heating, which is crucial for an application as actuator.
This extension makes it necessary to consider the balance of energy, which reads
It is readily interpreted as follows: the temperature in the wire changes due to
- heat exchange with the environment at temperature TE(t),
- the Joule heating j(t) produced by the electric current and
- the latent heats of the phase transitions. The third and fourth term on the R.H.S. of (5) H± represent the leading parts of the latent heat, and the last term is the part due to creation and annihilation of interfaces between austenitic and martensitic layers.
c is the specific heat and a the thermal conductivity coefficient.
The equations (3) and (5) together with (1) constitute a system of nonlinearly coupled ODEs and an algebraic relation. Together with appropriate initial conditions and prescribed heating function j(t), it can be solved for the resulting length change D(t) or, by inversion of (1), the load P(t). One of the two has to be known, however, and it follows from the coupling to the rernaining system.
page created on August 08, 1996 by A.Musolff
last update: April 13, 2005 by A.Musolff
© A. Musolff / SMAterial.com
URL:www.smaterial.com